Secure multi-party computation
Secure multi-party computation (also known as secure computation or multi-party computation (MPC)) is a sub field of cryptography. The goal of methods for secure multi-party computation is to enable parties to jointly compute a function over their inputs, while at the same time keeping these inputs private. For example, two millionaires can compute which one is richer, but without revealing their net worth. In fact, this very example was initially suggested by Andrew C. Yao in a 1982 paper.,[1] and was later named the millionaire problem.
The concept is important in the field of cryptography and is closely related to the idea of zero-knowledgeness. In general it refers to computational systems in which multiple parties wish to jointly compute some value based on individually held secret bits of information, but do not wish to reveal their secrets to one another in the process. For example, two individuals who each possess some secret information— and
and  , respectively—may wish to jointly compute some function
, respectively—may wish to jointly compute some function 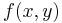 without revealing any information about
without revealing any information about  and
and  other than what can be reasonably deduced by knowing the actual value of
other than what can be reasonably deduced by knowing the actual value of 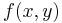 , where "reasonably deduced" is often interpreted as equivalent to computation within polynomial time. The primary motivation for studying methods of secure computation is to design systems that allow for maximum utility of information without compromising user privacy.
, where "reasonably deduced" is often interpreted as equivalent to computation within polynomial time. The primary motivation for studying methods of secure computation is to design systems that allow for maximum utility of information without compromising user privacy.
Secure computation was formally introduced in 1982 by A. Yao [2] (incidentally, the first recipient of the Knuth Prize) as secure two-party computation.
The millionaire problem and its solution gave way to a generalization to multi-party protocols.[3] In an MPC, a given number of participants p1, p2, ..., pN each have a private data, respectively d1, d2, ..., dN. The participants want to compute the value of a public function F on N variables at the point (d1, d2, ..., dN). An MPC protocol is dubbed secure if no participant can learn more from the description of the public function and the result of the global calculation than what he/she can learn from his/her own entry — under particular conditions depending on the model used.
Like many cryptographic protocols, the security of an MPC protocol can rely on different assumptions:
- It can be computational (i.e. based on some mathematical problem, like factoring) or unconditional (usually with some probability of error which can be made arbitrarily small).
- The model in which the scheme is described might assume that participants use a synchronized network (a message sent at a "tick" always arrives at the next "tick"), that a secure and reliable broadcast channel exists, that a secure communication channel exists between every pair of participants (an adversary cannot read, modify or generate messages in the channel), etc.
- The centrally controlled adversary considered can be passive (only allowed to read the data of a certain number of participants) or active (can corrupt the execution protocol or a certain number of participants).
- An adversary can be static (chooses its victims before the start of the multi-party computation) or dynamic (can choose its victims during the course of execution of the multiparty computation). Attaining security against a dynamic adversary is often much harder than security against a static adversary.
- An adversary can be defined as a threshold structure (meaning that it can corrupt or simply read the memory of a number of participants up to some threshold), or be defined as a more complex structure (it can affect certain predefined subsets of participants, modeling different possible collusions). These structures are commonly referred to as adversary structures. The opposite set consisting of the sets of honest parties that can still execute a computational task is related to the concept of access structures.
An important primitive in MPC is oblivious transfer.
Unconditionally or information-theoretically secure MPC is closely related to the problem of secret sharing, and more specifically verifiable secret sharing (VSS); many secure MPC protocols that protect against active adversaries use VSS.
Secure MPC provides solutions to various real-life problems such as distributed voting, private bidding and auctions, sharing of signature or decryption functions, private information retrieval, etc. The first large-scale and practical application of multiparty computation took place in Denmark in January 2008, as described by Bogetoft et al.[4]
Contents |
Two-party computation
The sub-problem of MPC that has received special attention by researchers because of its close relation to many cryptographic tasks is referred to as secure two-party computation (2PC) or just as Secure function evaluation (SFE). This area of research is concerned with the question: 'Can two party computation be achieved more efficiently and under weaker security assumptions than general MPC?'
Virtual Party Protocol
Virtual Party Protocol is an SMC protocol which uses virtual parties and complex mathematics to hide the identity of the parties.[5]
References
- ^ Andrew Chi-Chih Yao: Protocols for Secure Computations (Extended Abstract) FOCS 1982: 160-164
- ^ Andrew C. Yao, Protocols for secure computations (extended abstract)
- ^ O. Goldreich, S. Micali, and A. Wigderson. How to play ANY mental game. In Proceedings of the nineteenth annual ACM conference on Theory of computing, pages 218-229. ACM Press, 1987.
- ^ Peter Bogetoft and Dan Lund Christensen and Ivan Damgård and Martin Geisler and Thomas Jakobsen and Mikkel Krøigaard and Janus Dam Nielsen and Jesper Buus Nielsen and Kurt Nielsen and Jakob Pagter and Michael Schwartzbach and Tomas Toft: Multiparty Computation Goes Live, Cryptology ePrint Archive: Report 2008/068
- ^ Pathak Rohit, Joshi Satyadhar, Advances in Information Security and Assurance, Springer Berlin / Heidelberg, ISSN 0302-9743 (Print) 1611-3349 (Online), ISBN 978-3-642-02616-4, DOI 10.1007/978-3-642-02617-1
External links
- Solution to the Millionaire's Problem A description of Yao's algorithm
- Helger Lipmaa's links about multiparty computation
- Nick Szabo, "The God Protocols"
- Secure distributed CSP (DisCSP) solvers — a web-application with an applet-interpreter to design and run your own full-fledged secure multiparty computation (based on the SMC declarative language). Uses secure arithmetic circuit evaluation and mix-nets.
- VMCrypt A Java library for scalable secure computation. By Lior Malka.
- The Fairplay Project — Includes a software package for secure two-party computation, where the function is defined using a high-level function description language, and evaluated using Yao's protocol for secure evaluation of boolean circuits.
- The SIMAP project; Secure Information Management and Processing (SIMAP) is a project sponsored by the Danish National Research Agency aimed implementing Secure Multiparty Computation.
- Secure Multiparty Computation Language - project for development of a 'domain specific programming language for secure multiparty computation' and associated cryptographic runtime.
- VIFF: Virtual Ideal Functionality Framework — Framework for asynchronous multi-party computations (code available under the LGPL). Offers arithmetic with secret shared values including secure comparison.
- Sharemind: a framework for privacy-preserving data mining — A distributed virtual machine with the capability to run privacy-preserving operations. Has a privacy-preserving programming language for data mining tools. Includes developer tools.
- Virtual Parties in SMC A protocol for Virtual Parties in SMC (Secure Multi Party computation)
- MPC Java-based implementation A Java-based implementation of the MPC protocol based on Michael.B , Shafi.G and Avi.W's theorem ("Completeness theorems for non-cryptographic fault-tolerant distributed computation") with Welch-Berlekamp error correcting code algorithm to BCH codes. Supports multiple players and identification of "cheaters" with Byzantine protocol. By Erez Alon, Doron Friedland & Yael Smith.
- SEPIA A java library for SMC using secret sharing. Basic operations are optimized for large numbers of parallel invocations (code available under the LGPL).
- Essential bibliography Secure Multiparty Computation